Resampling in SimpleITK

SimpleITK has a fantastic python API for medical image processing, but it has a steep learning curve. In this post I will document how to resample images using the Resample filter via the complicated, but really useful task of extracting oblique slices in a 3D image. If you imagine a 3D image as a cube then an oblique slice is formed by sampling the image on a plane that has an arbitrary normal and does not align with the canonical axial, sagittal, coronal planes (see Fig. 1).

Figure 1 shows the typical setup in SimpleITK where the image field of view is denoted by the dotted cube. Let $\mathbf{p} = [p_x, p_y, p_z]$ be the physical coordinates of a point around which the oblique slice is centered. Let $\mathbf{x} = [x_1, x_2, x_3]$, $\mathbf{y} = [y_1, y_2, y_3]$, and $\mathbf{z} = [z_1, z_2, z_3]$ be the reference frame of the slice. $\mathbf{z}$ will also be the normal to the slice. For the sampled slice, let $\mathbf{o}$ be the SimpleITK origin of the slice (bottom left voxel).

I am assuming that we are given $\mathbf{p}$ and the unit vectors $\mathbf{x}$, $\mathbf{y}$, $\mathbf{z}$.

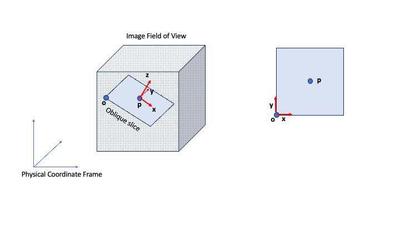
Given a SimpleITK img, I typically do the following to resample it:

resample = sitk.ResampleImageFilter()
resample.SetOutputDirection(output_direction)
resample.SetOutputOrigin(output_origin)
resample.SetOutputSpacing(output_spacing)
resample.SetSize(output_size)
resample.SetTransform(sitk.Transform())
resample.SetDefaultPixelValue(0)
resample.SetInterpolator(sitk.sitkLinear)
resample.Execute(img)

We have to specify the direction, origin, spacing, and size (in voxels) for the final resampled slice. direction in a SimpleITK header is a (9, 1)-shaped array that expresses the rotation matrix (in a row-major form) that takes the physical reference frame ($\mathbf{i} = [1, 0, 0]$, $\mathbf{y} = [0, 1, 0]$, $\mathbf{k} = [0, 0, 1]$) to the frame of the image.

Let the rotation matrix be $\mathbf{R}$, then notice that $\mathbf{R}\mathbf{k} = [r_{13}, r_{23}, r_{33}]$–the third column of $\mathbf{R}$. Applying the rotation $\mathbf{R}$ to the physical z axis should give us the new z axis which is $\mathbf{z}$. Therefore, we have $[r_{13}, r_{23}, r_{33}] = [z_1, z_2, z_3]$. Similarly the first and second columns of $\mathbf{R}$ will be $\mathbf{x}$ and $\mathbf{y}$ respectively.

R = np.zeros((3,3))
R[:,0] = x
R[:,1] = y
R[:,2] = z

The SimpleITK direction part of the header of the output slice will therefore be,

direction = $[r_{11}, r_{12}, r_{13}, r_{21}, r_{22}, r_{23}, r_{31}, r_{32}, r_{33}]$. Or in python:

output_direction = R.ravel()

or

output_direction_ = [x[0], y[0], z[0], x[1], y[1], z[1], x[2], y[2], z[2]]

To identify the physical coordinates of the origin $\mathbf{o}$ we have to do some vector arithmetic. From Figure 1, it is clear that

$\mathbf{o} = \mathbf{p} - d \mathbf{u}$,

where the unit vector $\mathbf{u}$ in the direction from $\mathbf{o}$ to $\mathbf{p}$ is given by $\mathbf{u} = \frac{\mathbf{x} + \mathbf{y}}{\sqrt{2}}$

$d$ is the distance between $\mathbf{o}$ and $\mathbf{p}$. If $w$ is the slice width, then $d = \frac{w}{\sqrt{2}}$. $w$ is in millimetres, so if the output slice size is in voxels $s$, then $w = s * r$, where $r$ is the voxel spacing in millimetres. Here we assume that we have the same voxel spacing in x-y directions.

u = (x + y)/np.sqrt(2)
d = (s * voxel_spacing)/np.sqrt(2)
output_origin = p - d*u

That’s about it. We can specify the rest of the output image parameters and execute the resample filter to extract an oblique slice centered at a point $\mathbf{p}$ and oriented along the frame $\mathbf{x}-\mathbf{y}-\mathbf{z}$, with the slice normal being $\mathbf{z}$.

SimpleITK has a nice set of notebooks here and perhaps if I had done the homework exercises my learning curve would not have been so steep.